딥러닝 파이토치 교과서 Ch.12
강화 학습(reinforcement learning)
정의
- 어떤 환경에서 어떤 행동을 했을 때 그것이 잘된 행동인지 잘못된 행동인지를 판단하고
보상(또는 벌칙)을 주는 과정을 반복해서 스스로 학습하게 하는 분야. - 어떤 환경 안에서 정의된 에이전트가 현재의 상태를 인식하여, 선택 가능한 행동들 중 보상을 최대화하는 행동 혹은 행동 순서를 선택하는 방법. 최적의 (Optimal Policy)

개념
- 강화 학습의 목표는 환경과 상호 작용하는 에이전트를 학습시키는 것.
- 환경
에이전트가 다양한 행동을 해 보고, 그에 따른 결과를 관측할 수 있는 시뮬레이터.
환경은 주로 마르코프 결정 과정으로 주어짐. - 에이전트
환경에서 행동하는 주체. (게임에서 게임기-환경, 게임하는 사람-에이전트) - 상태
에이전트가 관찰 가능한 상태의 집합. 시간에따라 달라짐 - 에이전트는 다양한 상황 즉, 상태 안에서 행동(action)을 취하며, 조금씩 학습해 나가고
에이전트가 취한 행동은 그에 대한 응답으로 양(+)이나 음(-) 또는 0의 보상(reward)을 돌려받게됨.
마르코프 결정 과정 (Markov Process, MP)
- 강화 학습은 마르코프 결정 과정에 학습 개념을 추가한 것. 강화 학습의 문제들은 마르코프 결정 과정으로 표현하고, 이 마르코프 결정 과정은 모두 마르코프 프로세스에 기반
- 강화 학습은 마르코프 결정 과정에 대한 지식을 요구하지 않고, 크기가 매우 커서 결정론적 방법을 적용할 수 없는 규모의 마르코프 결정 과정 문제를 다룬다는 점이 기존과의 차이.
개념
- 마르코프 프로세스
어떤 상태가 일정한 간격으로 변하고, 다음 상태는 현재 상태에만 의존하는 확률적 상태 변화를 의미.
즉, 현재 상태에 대해서만 다음 상태가 결정되며, 현재 상태까지의 과정은 전혀 고려할 필요가 없음.
변화 상태들이 체인처럼 엮여 있다고 하여 마르코프 체인(Markov chain)이라고도 합니다. - 마르코프 특성(Markov property)을 지니는 이산 시간(discrete time)에 대한 확률 과정(stochastic process).
확률 과정 = 시간에 따라 어떤 사건의 확률이 변화하는 과정.
이산 시간 = 시간이 연속적이 아닌 이산적으로 변하는 것. - 마르코프 특성은 과거 상태들(S1, …, St-1)과 현재 상태(St)가 주어졌을 때, 미래 상태(St+1)는 과거 상태와는 독립적으로 현재 상태로만 결정된다는 것을 의미. 즉, 과거와 현재 상태 모두를 고려했을 때 미래 상태가 나타날 확률과 현재 상태만 고려했을 때 미래 상태가 발생할 확률이 동일하다는 것.

- 전이(transition)
마르코프 체인은 시간에 따른 상태 변화를 나타냄. 상태 변화를 전이라고 함. - 상태 전이 확률(state transition probability)
전이는 확률로 표현하며 이를 상태 전이 확률이라 함. - 시간 t에서의 상태를 s, 시간 t+1에서의 상태를 s'라고 할 때 수식.

- P(A|B)는 조건부 확률로 B가 발생했을 때 A가 발생할 확률. 병원 방문 예시.
각각의 상태에서 다른 상태로 이동할 확률의 합은 1로 상태가 이어져 있음. - 일반적으로 상태는 원으로 표기하고, 종료(terminal) 상태는 사각형으로 나타냄.
종료 상태에 들어가면 다른 상태로의 이동은 X.
숫자가 한 상태에서 다른 상태로 변이하는 확률



생각해보기 (https://bskyvision.com)
이번 주에 코카콜라를 사마신 사람의 80%가 다음 주에도 역시 코카콜라를 사마신다.
나머지 20%는 마음이 바뀌어 펩시콜라를 사마신다.
이번 주에 펩시콜라를 사마신 사람의 70%가 다음 주에도 역시 펩시콜라를 사마신다.
나머지 30%는 마음이 바뀌어 코카콜라를 사마신다.
이번 주에 10억명이 코카콜라를 마셨고, 8억명이 펩시콜라를 마셨다고 할 때, 10주 후와 50주(약 1년) 후에 코카콜라, 펩시콜라를 마시는 인구는 각각 어떻게 될까?
(전세계에서 콜라를 마시는 인구는 18억명이라고 가정했고, 또한 비(非)콜라인 중에 새롭게 콜라를 마시기 시작하는 사람은 없다고 가정한다.)
마르코프 보상 프로세스 (Markov Reward Process, MRP)
- 마르코프 프로세스에서 각 상태마다 좋고 나쁨(reward)이 추가된 확률 모델
- 어떤 상태에 도착하게 되면 그에 따르는 보상을 받게 되는 것
- 모든 보상의 합 = 리턴



- 어느 시점에서 보상을 받을지가 중요
특정 상태에 빨리 도달해서 즉시 보상을 받을 것인가 OR 나중에 도달해서 보상을 받을 것인가 가치 판단 필요. - 이자 예시. (현재 가치)에 (이자: 현재 가치×이자율)을 더하면 (미래 가치). (현재 가치)와 (미래 가치)를 비교하기 위해서는 시간 개념이 필요. (현재 가치)는 t 시간이고 (미래 가치)는 t 시간보다 더 미래의 시간이라고 했을때, 미래 가치는 t 시간으로부터 충분히 시간이 지나고, 그에 따른 이자가 붙어야만 현재 가치와 동일해짐.
즉, 미래 가치를 현재 시점으로 보면 현재 가치보다 적은 것. - 할인율(discounting factor, γ)
보통 γ는 0과 1 사이의 값으로 하여 미래 가치를 현재 시점에서의 가치로 변환.
할인율이 0에 가까울 수록 다음 보상 추구(근시안적), 1에 가까울 수록 미래 보상 고려(원시안적). - 가치 함수
가치 = 현재 상태가 s일 때 앞으로 발생할 것으로 기대되는(E) 모든 보상의 합
가치 함수는 현재 시점에서 미래의 모든 기대되는 보상을 표현하는 미래 가치.
따라서 강화 학습의 핵심은 가치 함수를 최대한 정확하게 찾는 것.
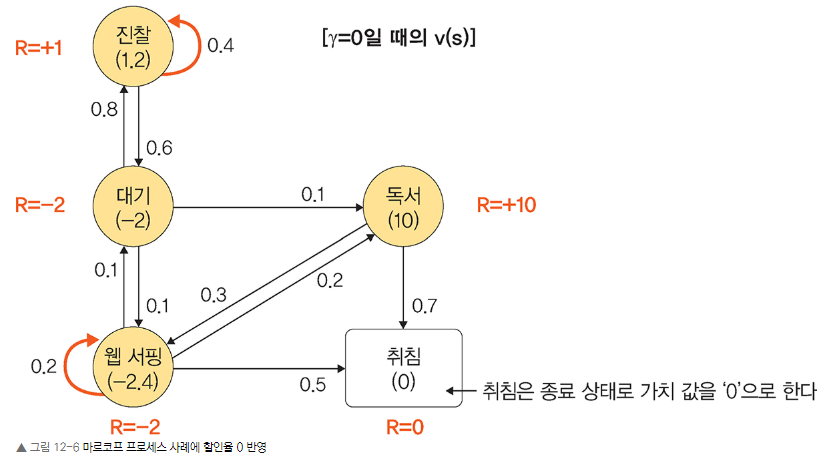

마르코프 결정 과정 (Markov Decision Process, MDP)
- 기존 마르코프 보상 과정에서 행동이 추가된 확률 모델
- 정의된 문제에 대해 각 상태마다 전체적인 보상을 최대화하는 행동이 무엇인지 결정하는 게 목표.
- 행동 분포(행동이 선택될 확률)를 표현하는 함수 = 정책(policy, π)
π는 주어진 상태 s에 대한 행동 분포를 표현한 것
가치 함수
상태-가치 함수(vπ(s))
- 에이전트가 놓인 상태 가치를 함수로 표현한 것.
- 상태 s에서 얻을 수 있는 리턴의 기댓값
- 주어진 정책(π)에 따라 행동을 결정하고 다음 상태로 이동한다는 점이 MRP와 다름
행동-가치 함수(qπ(s,a))
- 행동에 대한 가치를 함수로 표현한 것.
- 상태 s에서 a라는 행동을 취했을 때 얻을 수 있는 리턴의 기댓값.
- 가치 함수를 계산하는 방법은 O(n^3)의 시간복잡도로 상태 수가 많으면 적용이 어려움.
- 학습 효율을 높이는 방법
다이나믹 프로그래밍, 몬테카를로, 시간차 학습, 함수적 접근 학습
'AI' 카테고리의 다른 글
| 생성모델 (0) | 2023.08.06 |
|---|---|
| ViT (0) | 2023.08.06 |
| Transformer (0) | 2023.06.25 |

